はじめに
今回は関数電卓の使い方_初級編!
のお話をしていきたいと思います♪
最初にお伝えしておきますが
今回の内容は初級編ということで
あくまでも土木技術者になったばかりの方や
土木技術者になって1年程度たった人むけ
になっていますので
もう使いこなしているよって人は
ここで読むのをやめてください(笑)
時間の無駄ですよ(;´Д`)
読みすすめてもらっているってことは
土木技術者になって1年程度の方ばかりと思います!
一緒に学んでいきましょう♪
では早速、解説する視点と条件は
建設会社に勤める
1〜2年目の土木技術者
で
使用する電卓は「CASIO」さんの
関数電卓を用いて解説します!
CASIOさんの関数電卓を利用する理由は
単純にぼくが長年つかっているからです(笑)
関数電卓の使い方_初級編!
- 三角関数 sin cos tan
- 三角関数 sin-1 cos-1 tan-1
- 三平方の定理

いやいやまってくださいよ!
そんなの土木技術者では
あたりまえではないですか?



なるほどっ!
まぁそこで
ぼくの意見ですが
おっしゃるとおり
土木技術者としては使えて
当たり前といえば当たり前ですが
人材不足が叫ばれる建設業においては
土木工学科や理系出身の学生さん以外から
入職される人が増加しています!
そのような人がいきなり現場で
関数電卓を活用するのってめっちゃ大変です!
そこで今回のような
関数電卓の初歩をYouTube動画で
学べたらえぇなぁ〜と考え動画にしました^_^


三角関数
本題にはいる前に
すこしおさらいです♪
三角関数の基本は
数学の考え方にもとづいて
直角三角形をつくって考える
ですね!
まずsinθの
計算のやり方は「Sを描くイメージで」
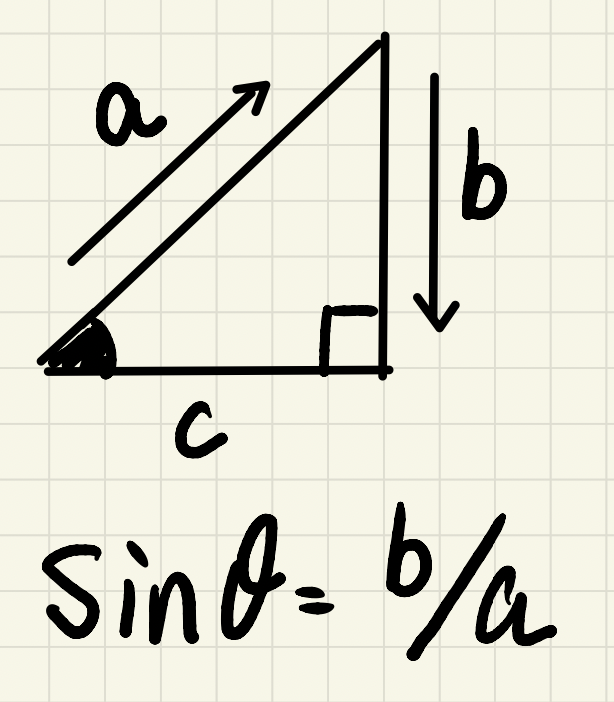
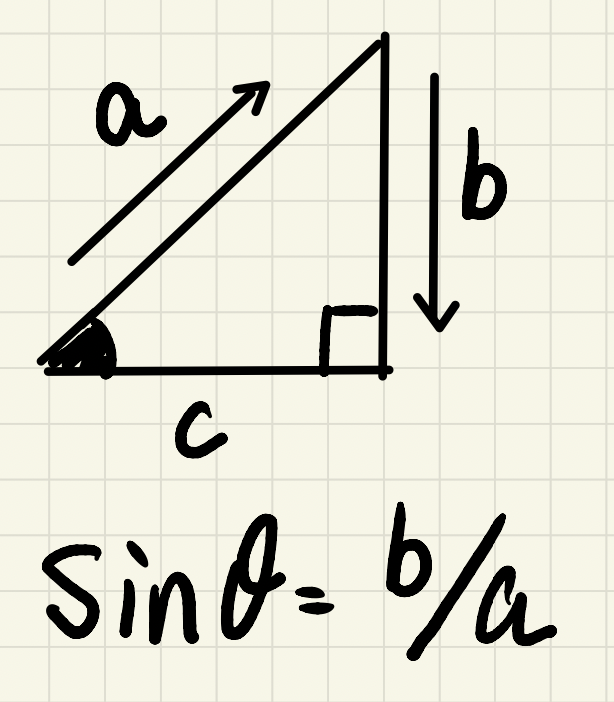
つぎにcosθの
計算のやり方は「Cを描くイメージで」
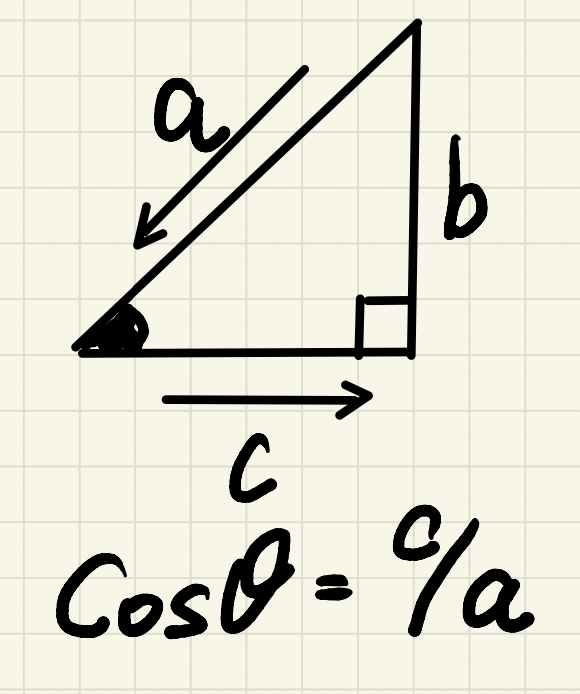

最後にtanθの
計算のやり方は「tを描くイメージで」
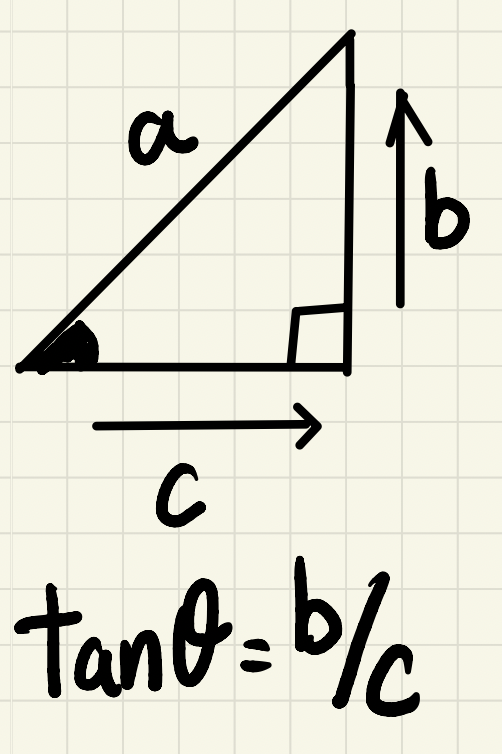

学生時代にならった上↑の式を
つかって計算していきます!
いやな思い出があるかもですが(笑)
くじけずに前を向いていきましょう♪


sin cos tan
では早速1つめからいきましょう♪
まず例題1は
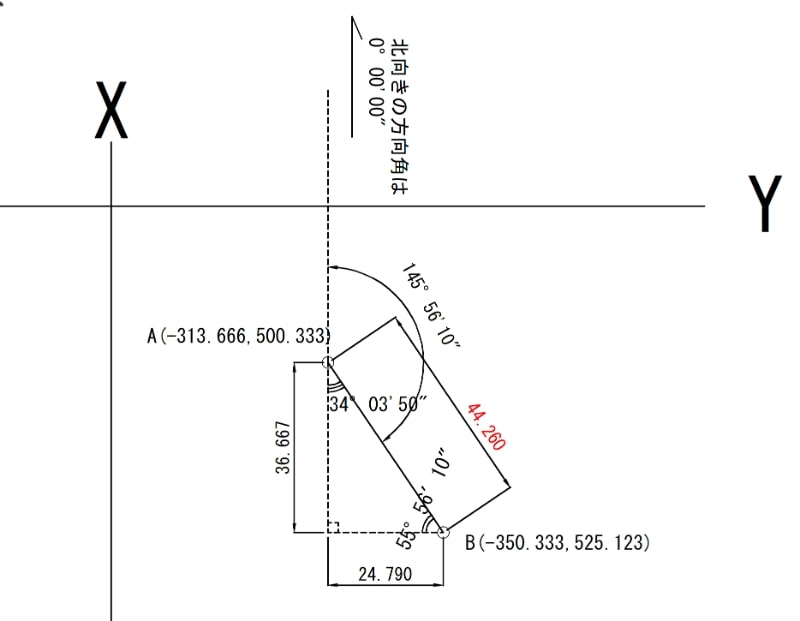

斜部分の44.260を計算していきます♪
44.260を「X」に置き換えて計算しますね
つかう公式はsinθの式をつかいつつ
考え方を図にあらわすと
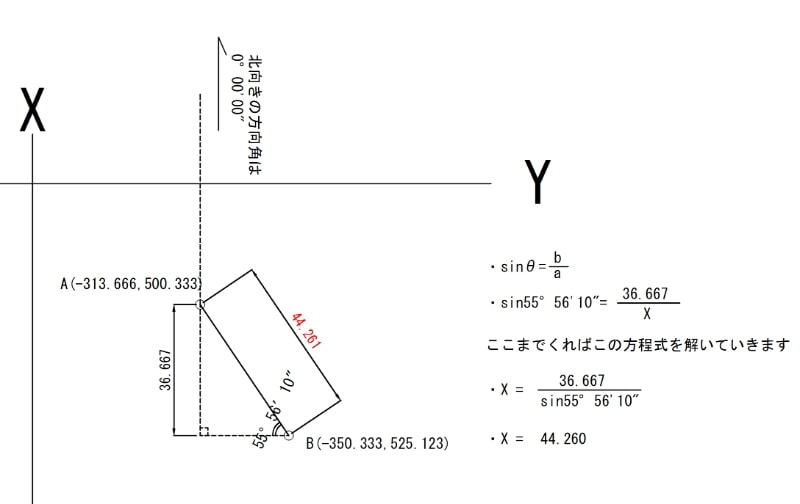

図を踏まえて
実際に関数電卓をたたいてみましょう♪
たたく式は
X=36.667 / sin55°56’10”
になります♪
あくまでもCASIO製の関数電卓ですが
実際にたたいてみます
①:「36.667」をおす

②:「割り算 /」をおす

③:「sin55°56’10″」をおす


④:「=」をおす


⑤:「44.261」が表示されたら正解
「44.261」が表示されたら正解です
少し補足ですが
1mm(ここでいうと0.001)程度の誤差は発生してもOKです♪
小数点以下の掛け算とわり算なので
1mm程度の誤差はこの際、無視してください♪
以上ここまでは
sin cos tanをつかった関数電卓を使い方を解説しました
sin-1 cos-1 tan-1
つぎに「アークsin」「アークcos」「アークtan」の計算にいきましょう!
-1乗の読み方を「アーク」とよみます♪
これは
例題1とは逆に長さはわかってるけど
角度(θ)がわからんねんって時に使います
では早速例題2をしめすと
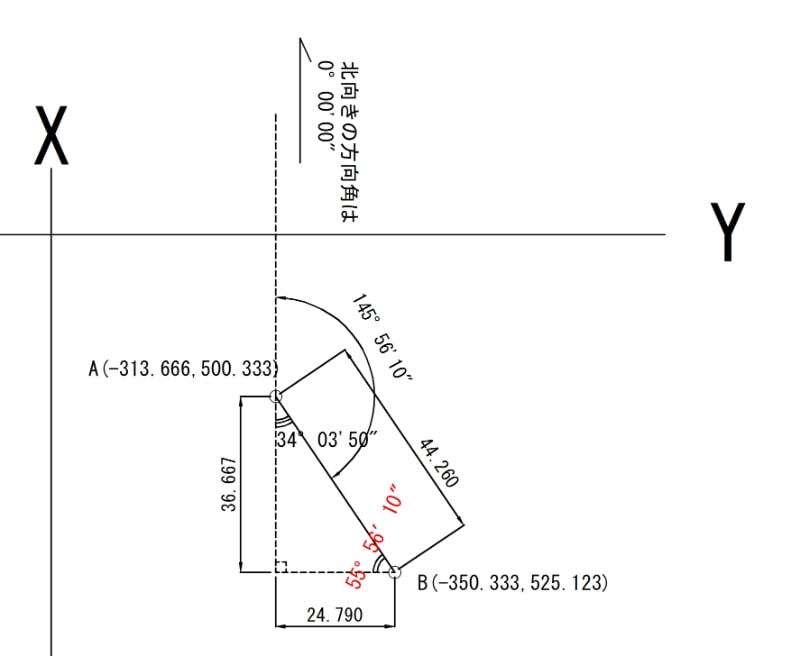

右下の「55°56’10″」の角度を「X」と仮定して計算していきます♪
くじけずについてきてくださいね(笑)
つかう公式はcosθの式を使いつつ
考え方を図にあらわすと
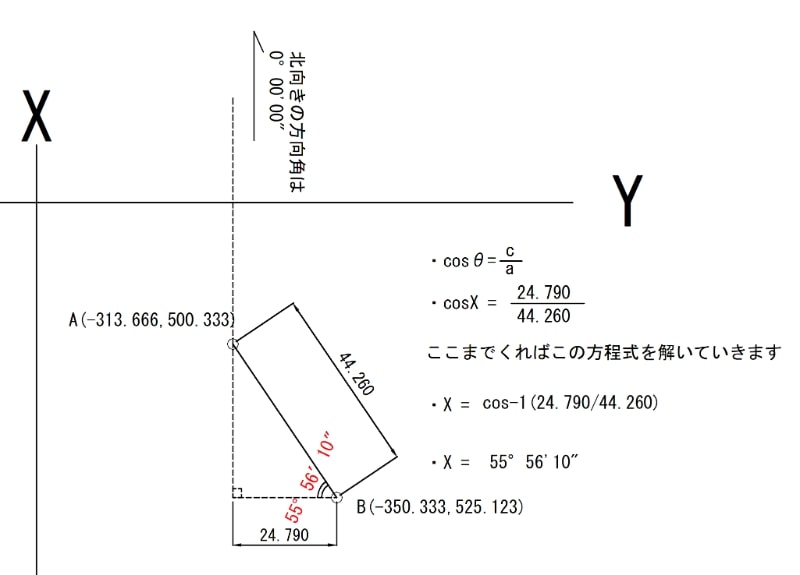

図を踏まえて
実際に関数電卓をたたいてみましょう♪
たたく式は
X=cos-1 ( 24.790 / 44.260 )
CASIO製の関数電卓の前提で
実際にたたいてみます
①:「シフト」「cos-1」をおす
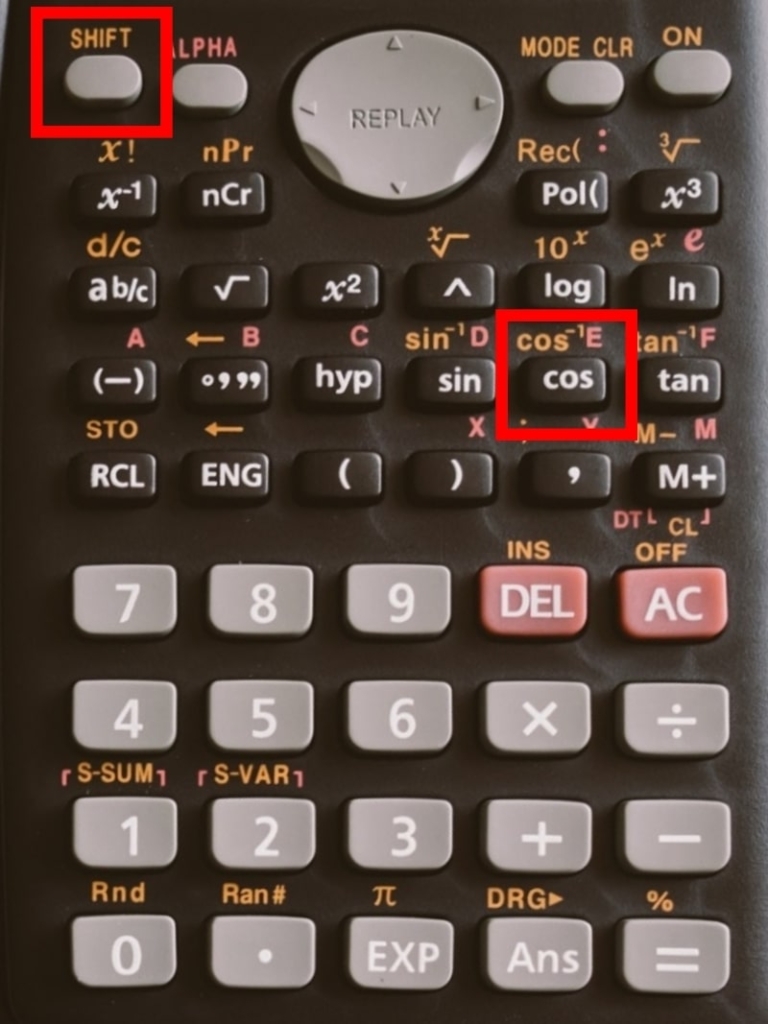

②:「(24.790/44.260)」をおす
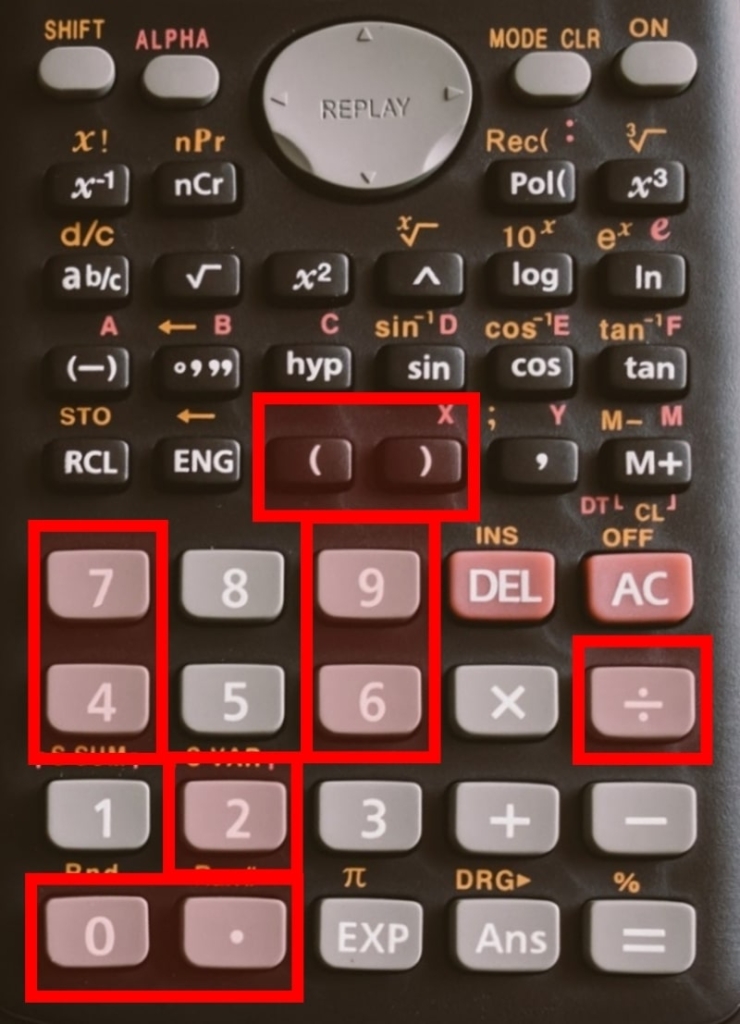

③:「=」をおす
④:「55.93732694」が表示されたら正解
⑤:「55.93732694」が表示されている状態で「° ‘ “」をおす


※ここでも少し補足です♪
この「°′′′」ボタンを押す意味は
0進法から60進法へ変換しないと角度表示にならない
からになります^^;
ちょっと複雑ですが
角度表示は時計と同じ考えってことは
覚えていってくださいね^_^;
⑥:「55°56’14.38″」が表示されたら正解
以上ここまでは
「sin-1 con-1 tan-1」をつかった関数電卓を使い方を解説しました
三平方の定理
さいごに三平方の定理を
解説しておわりにします♪
最後まで頑張ってついてきてくださいね^^
早速例題をしめすと
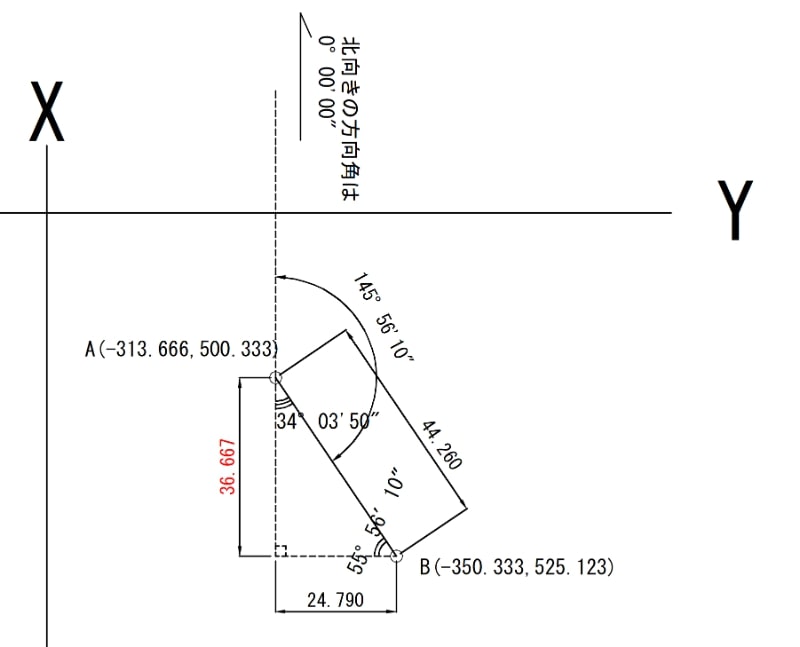

縦部分の長さ「36.667」を「X」と仮定してを計算していきます♪
計算の前に使う公式は
直角三角形において
「縦の2乗 + 横の2乗 = 斜の2乗」
この公式をつかって計算します
さっきの三角関数にくらべると簡単でしょ???
この公式をつかいつつ
考え方を図にあらわすと
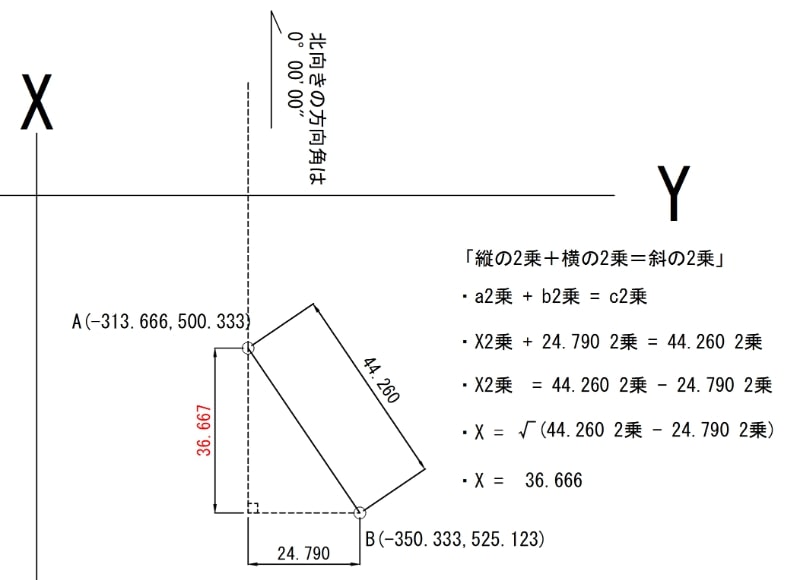

図を踏まえて
実際に関数電卓をたたいてみましょう♪
たたく式は
X=√(44.260 2乗 – 24.790 2乗)
CASIO製の関数電卓の前提で
実際にたたいてみます
①:「√ルート」をおす


②:「(44.260の2乗」をおす
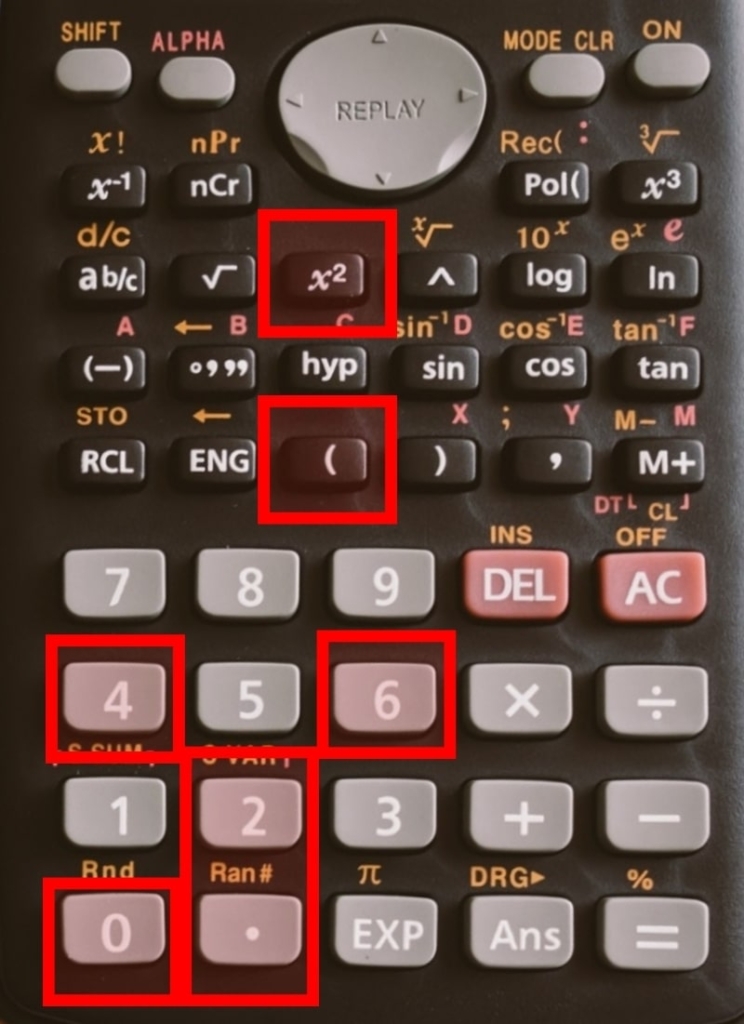

③:「- 24.790の2乗)」をおす
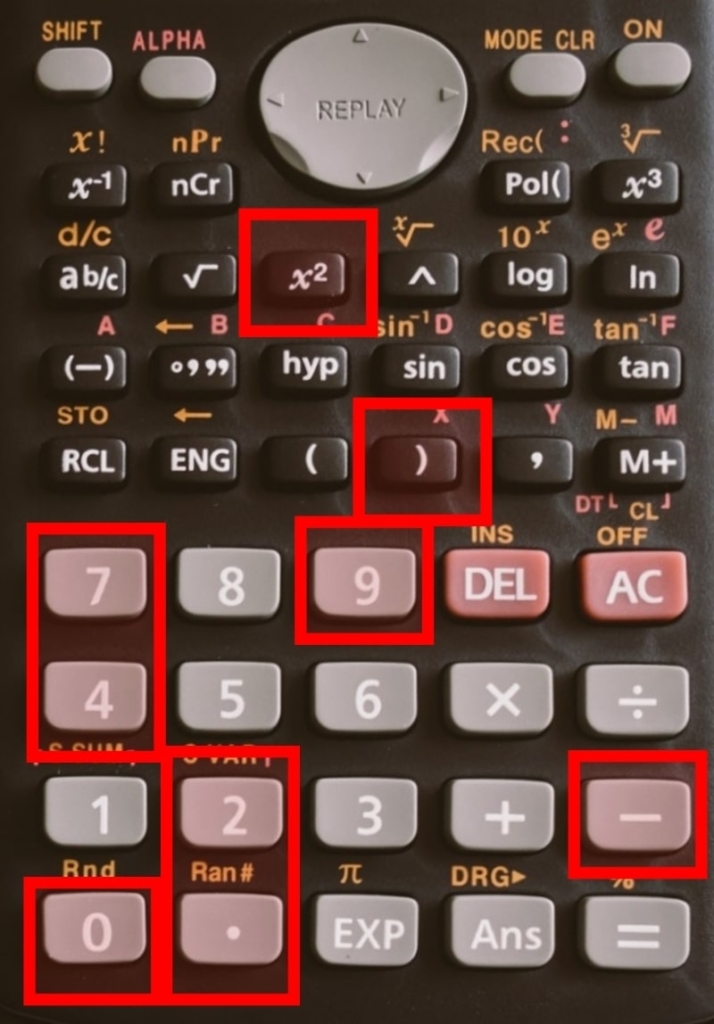

④:「=」をおす
⑤:「36.666」が表示されたら正解
ここでも少し補足ですが
1mm(ここでいうと0.001)程度の誤差は発生してもOKです♪
小数点以下の掛け算とわり算なので
1mm程度の誤差はこの際、無視してください♪
以上ここまでは
「三平方の定理」をつかった関数電卓を使い方を解説しました
おわりに
今回は関数電卓の使い方_初級編!
のお話でした♪
勢いで建設業界に飛び込んではみたが関数電卓ってなに?
って人にむけた内容でしたがいかがだったでしょうか???
ブログの感想もTwitterなどで聞かせてもらえれば嬉しいです^^
また次回のブログでお会いしましょう♪
ではでは

